Energy-Based Learning for Cooperative Games, with Applications to Valuation Problems in Machine Learning

Yatao Bian¹, Yu Rong¹, Tingyang Xu¹, Jiaxiang Wu¹, Andreas Krause², Junzhou Huang^1
1Tencent AI Lab
²ETH Zurich

ICLR 2022

Project Description

Valuation problems, such as feature interpretation, data valuation and model valuation for ensembles, become increasingly more important in many machine learning applications. Such problems are commonly addressed via well-known game-theoretic criteria, such as the Shapley value or Banzhaf value. 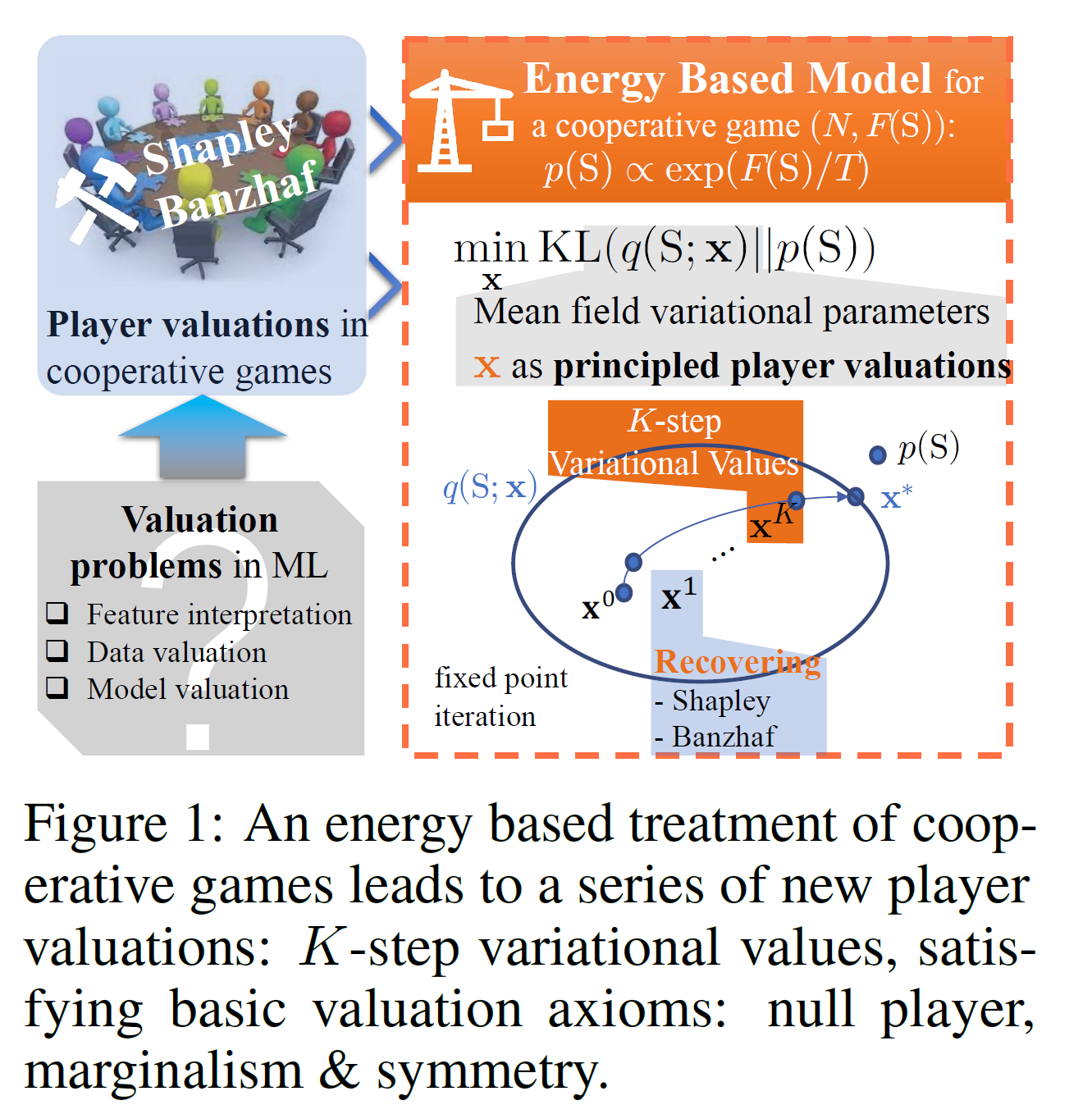In this work, we present a novel energy-based treatment for cooperative games, with a theoretical justification by the maximum entropy principle. Surprisingly, by conducting mean-field variational inference of the energy-based model, we recover classical game-theoretic valuation criteria through conducting one-step fixed point iteration for maximizing the ELBO objective. This observation also verifies the rationality of existing criteria, as they are all attempting to decouple the correlations among players. By running the fixed point iteration for multiple steps, we achieve a trajectory of the variational valuations, among which we define the valuation with the best conceivable decoupling error as the Variational Index. We prove that under uniform initializations, these variational valuations all satisfy a set of game-theoretic axioms. We empirically demonstrate that the proposed Variational Index enjoys lower decoupling error and better valuation performance on certain synthetic and real-world valuation problems.

Paper

• ICLR 2022: https://openreview.net/forum?id=xLfAgCroImw

Video, Poster and Slides

• Video: https://iclr.cc/virtual/2022/poster/6807

• Poster: https://yataobian.com/docs/val-game-poster-v2.png

• Slides: https://yataobian.com/docs/valuation-game-slides-v3.pdf

Code

• Code: https://github.com/tencent-ailab/valuationgame

Contact

Yatao Bian https://yataobian.com